写在前面

最近一段时间也集中刷了一些搜索的入门题，感觉应该对搜索问题进行一次总结。所以此篇博文是我针对写的题的简单分析，错误无法避免，如果发现欢迎留言改正。另外，由于是分析类的博文，所以代码会很少，算法的代码和题解这里不会出现哒^_^。如果对BFS和DFS的代码都不会，还是推荐学习一下图论以及具体代码，下面写的都是思想了（口胡技能EX）

搜索基本算法：BFS与DFS

关于BFS与DFS，即广度优先搜索与深度优先搜索。由于重点不在这两个算法的具体实现，这里就简单写一下这两种算法的思想好了。

DFS

DFS，用迷宫类比是很恰当的。一般人在考虑走迷宫的时候是先直接走，碰见岔路的时候选择其中一条继续走，再碰见岔路就继续走，直到碰见死路或者走出迷宫。走出迷宫就不说了，碰到死路的时候，一般人都是往回退，退到岔路口选择另外一条路再继续走。就这样，直到出迷宫。

在这个过程中，我们对于路线有2种处理：

记录路线，方便往回走，以及哪个地方走过哪个地方没走过。
记录岔路口，方便确定该回退到哪里有岔路。

很明显，是递归与回溯的问题。我们可以用数组来储存走过的地点防止重复，同时，每次走的时候都建立成递归的方式，这样如果走出迷宫，没什么好说的；如果没走出迷宫，直接回溯，能够回溯到上一次有岔路的地方，并且由于数组记录了走过的路，所以一定走的是岔路的另一条没走过的路。

确定走出迷宫很简单，出去就是出去了，之前的所有数据都不管。

如果没有走出，一定是在回溯的时候发现：已经没有岔路好选了。

这里注意一点，回溯的时候是一层一层向上回的。上一个岔路没有路可以走就继续向上回，直到第一个岔路仍然无路可走（也就是回溯到最初的函数），就说明搜索失败。

BFS

BFS，用迷宫类比不太恰当，因为正常人不会选择在走迷宫的时候“广搜”。

假设你站在岔路口，DFS是先随便找一条路走走看，出去就出去，出不去返回岔路口重来。但是BFS就是先选一条路走，走两步，再拐回来选另一条路走两步，在拐回来。

所以我们用棋盘涂色来类比BFS。看下图：

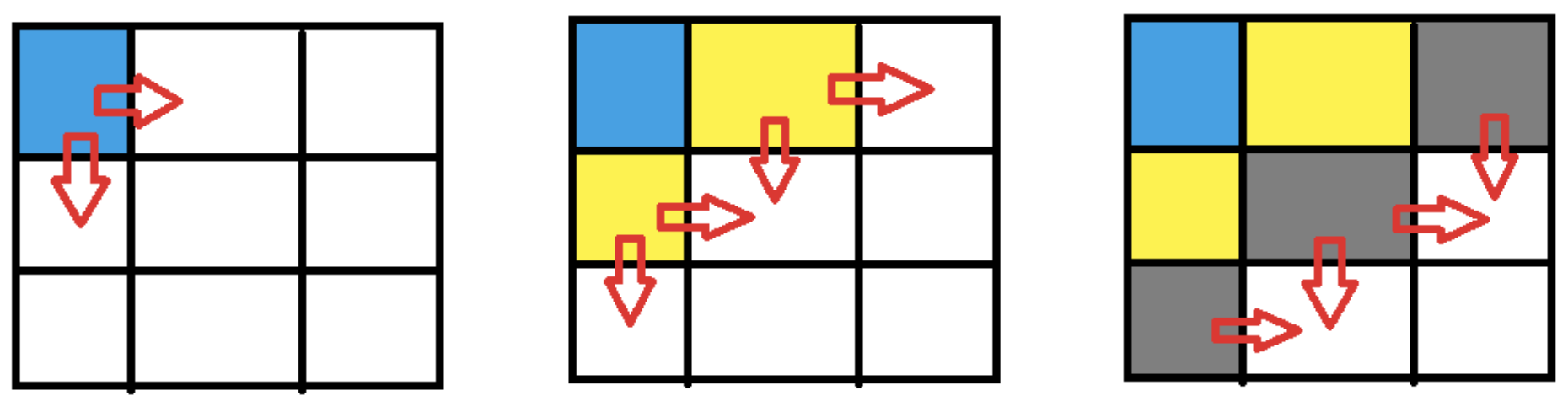
在涂色的时候，我们从左上角开始涂，然后涂紧挨着这个地方的方块，然后继续，再图紧挨着的方块。

那么在这个过程中，我们对整块棋盘有这2步处理：

将当前方块的紧挨着的方块涂色，同时记录已经涂过色的方块。
记录新出现的方块，这样才能涂新的方块。

为了实现这些操作，除了创建一个数组存放已经遍历过的方块，我们还需要一种数据结构，要求将最外面的方块存放，当需要涂色的时候取出这个方块，并对其四周进行处理——栈，很方便完成我们的想法。

以上，我们可以确定储存已经遍历过的位置可以单独开一个数组来存放，BFS使用栈来处理，DFS利用递归与回溯。具体的实现如果不会的话可以去百度了，博主就不贴代码啦。

BFS与DFS的选择以及两者的优缺点

bfs与dfs的选择是很重要的问题，虽然两者都是搜索，但是根据问题的不同两者在在使用上、耗费的时间都有非常大的不同。

BFS选型分析

BFS是用来搜索最短径路的解是比较合适的，比如求最少步数的解，最少交换次数的解，因为BFS搜索过程中遇到的解一定是离根最近的，所以遇到一个解，一定就是最优解，此时搜索算法可以终止。

这个时候不适宜使用DFS，因为DFS搜索到的解不一定是离根最近的，只有全局搜索完毕，才能从所有解中找出离根的最近的解。

DFS选型分析

DFS适合搜索全部的解，因为要搜索全部的解，那么BFS搜索过程中，遇到离根最近的解，并没有什么用，也必须遍历完整棵搜索树，DFS搜索也会搜索全部，但是相比DFS不用记录过多信息，所以搜素全部解的问题，DFS显然更加合适。

空间优劣上，DFS是有优势的，DFS不需要保存搜索过程中的状态，而BFS在搜索过程中需要保存搜索过的状态，而且一般情况需要一个队列来记录。

两种搜索怎么选？

一些问题会针对于这些浅显易懂的优缺点下手，例如求最短路类的问题，如果用DFS仍然不是TLE就要怀疑数据太水或者是签到题了。当然这些问题都是相对简单的。

大部分题目考虑了两者的优缺点，但是实际上是两者都可以使用，具体怎么用着方便就仁者见仁智者见智了。因为两者的框架与思路不同，根据不同的要求选择某一种方法会明显顺畅许多。所以大部分题目虽然都是搜索，但是会发现discuss里大部分讨论的都是某一种方法（当然大佬一般都使用骚算法1A带走，顺便验证真理——我做的题都是水题）。下面博主会分析一下两者的选择。

一些选型示例与编码重点

最短路问题

最短路问题果断选择bfs，这个就没必要解释了，当然，如果数据量小同时dfs算法还简单粗暴的情况下dfs也未尝不可，只是碰见的几率着实不高。bfs在整体上有几个非常重要的点：

使用队列。
层次分明，如果构造搜索树的话，bfs是按层遍历的。
不使用递归和回溯。

所以说bfs不适合大范围搜索，或者说不适合需要得到路径的问题，但是非常适合复杂的数据结构以及有特殊要求的问题。

一个结构体，然后扔在queue中就好了，每次的操作也是非常简单的判定，判断某个状态是否能存在，能存在就将该状态扔进queue，不能则不用管。搜索到结果直接结束搜索。

特殊要求是指关于排序方面的问题。因为我们使用队列，那么当然也能使用优先队列了。

常规的排序方式可以对结构体重载操作符实现，复杂一点的比如路径花费问题，能走3种方向，但是每个方向的花费不同，那么果断优先队列啊，否则就算找到最短路也不一定是花费最短的路。如果是bfs，再考虑建立cost数组就将问题复杂化了。

DP/划分子问题的搜索

dfs对博主而言，感觉上是比bfs难的。

bfs只用考虑一点——如何走就行。dfs有很重要的一点是考虑划分子问题。只要跟递归有关就要考虑子问题的划分。（有时候分着分着就把dp的状态转移方程写出来了- -）。

最优解的问题以及路径问题一般也是使用dfs。

这里注意，博主说的最优解跟最短路是不一样的，也跟花费没有太大关系。这里的最优解其实跟dp问题有点类似了，当前的选择会影响后面的问题。所以说dfs相关问题很大程度上能变成dp问题。dfs主要的点是：

回溯与递归
剪枝非常方便，因为划分成了子问题，剪枝会变得很简单。

所以说很多复杂问题还是能够构造成dfs的思路的。尤其是因为dfs的算法实现了递归，所以不仅剪枝相对容易（因为是单独的小问题考虑，剪枝要求再多也是多写几个判断而已），在路径的统计问题上也比bfs好很多。

同时可以有两套相关操作：递归时一套，回溯时一套。

比如要求总共走多少步的时候可以定义全局变量，递归时count++，回溯时count++。

有特殊的要求比如回来时花费的精力要高于探索的时候，也是递归一套标准回溯一套标准。

BFS模型的框架与分析

关于dfs的模型框架，我们分成2部分：

在进入bfs函数前，建立好队列以及结构体。

a> 一般来说，我们把图的节点存在结构体中（一般不会出简单的搜索，各种限制条件，坐标数量，需要用结构体以及泛型）。

b> 建立queue，同时将起点储存在队列中。
进入bfs函数。

框架如下：

void bfs(队列que) {
    while (队列不为空) {
        取出队列头
        if (满足搜索条件) 结束搜索;
        for (迭代下一步移动方式) {
            建立下一步移动的位置数据
            if (检查是否满足条件) {
                满足条件，处理数据
		将该步放进队列
            }else continue;
        }
    }
    return;
}

当然，实际上我们会有很多不同的写法。

例如队列，我们可以传参，但是博主个人更喜欢将队列写入全局变量，这样方便main函数中进行处理。

或者写进bfs函数中，可以免去初始化的烦恼。

bfs的返回值可以不怎么考虑。如果有返回值也是在答案要求单一的情况下可以这样处理。实际上将答案储存在全局变量中也未尝不可。

DFS模型的框架与分析

dfs算法的核心部分是利用递归，在搜索问题建立模型的时候主要考虑搜索的结果。这也是dfs跟bfs的主要区别：dfs重点在于全搜，bfs重点在于搜最短。

dfs的模型一般是求方案。例如从A点到B点有几种走法。要求暴力搜索全部可能。或者要求的结果基本上是将图搜索了一遍甚至多遍。此时使用dfs的递归就非常简单易懂。框架如下：

void dfs(){
	if(满足条件，或者说找到了该可能){
		处理这种可能
	}
	各种剪枝
	for(遍历下一步的可能){
		假设有n种可能，这里开始第i种可能
		dfs(); 递归进入该可能的情况
		假设不从i进行，而是继续遍历走其他的可能
	}
	完全不考虑这个节点，直接进行下一步。或者是结束整个寻找。
}

其实博主这个框架并不好。因为dfs的情况真的多，感觉并不好描述。或者说dfs相比bfs要灵活很多，不能用一种统一的方式来描述这个过程。

下面是博主对这个框架的额外解释与分析。

DFS 参数问题

一般来说，dfs是要有参数的。参数非常非常重要，就好比在写递归的时候难道要将各种变量定义成全局么？不是说变量是全局就无法使用递归，而是说没有用到递归最妙的部分——利用上一步的值来处理，最终回溯。

dfs亦然。dfs在构造成搜索树的时候也是非常简单明了的，我们在路径搜索以及输出的时候，完全可以将树的深度作为参数，这样就可以得到每个树枝（一条树枝就是一个解，有的树枝需要剪枝）的前后关系。

这个关系可以利用回溯进行额外处理，或者就是再递归的时候存入栈或者数组。

总之，参数列表很重要。下面的文章也会给出一些问题，凸显了参数列表的作用。

DFS 划分子问题

dfs的状态转移也是相当重要的。

没错，这里的状态转移跟dp的如出一辙。很多dp的问题说白了就是暴力搜索+剪枝，枚举可能嘛。

dp的前一个操作对后面的操作无影响，但是影响了后面问题的规模。那么不也是搜索树的模型么，当前节点的处理跟后面节点的处理没有任何关系，但是当前节点的规模却决定了后面的树的深度。

所以划分子问题是dfs的精髓。不能说看到搜索路径，好啊先走一波dfs试试，然后连状态转移都没规划好。

一般需要考虑状态转移的dfs是线性问题。例如有n个加油站，加油需要耗费时间，如果路上没有就gg。求一种加油方式可以耗费最少时间到达终点。这种问题可以理解成dp，当然也可以写成搜索。本质上可以划分成在第k个加油站加油，后n-k个加油站是一个划分。

dfs并不是简单的递归就行了，还要考虑是否走这一种情况。进入下一层函数的语句作为分界线，上面是递归下面是迭代。

有的时候，例如迷宫找路，我们在回溯以后再运行，实际上这个时候我们运行的前提是根本没有进入递归。

以上面提到了加油站为例子，我们可以写出这样的代码：

for(迭代，在第i个加油站加油){
    加满油
    dfs(如果在第i个加油站加油，进入该子树)
    此时需要将油箱的油还原到加油前
}

因为我们已经回溯了，回溯到了第i个加油站的位置，如果加油——进入子树，或者说分支。那么回溯回来以后我们的代码还是要运行的，继续运行的是不加油的操作。

加油跟不加油是两个操作，还原的操作一定不能忘记。一般来说，我们写搜索都需要辅助数组，记录已经走过的位置，当然这里辅助数组最好还是还原的。

DFS 的递归

为什么要递归？就是一个暴力搜索的过程，对于A点，有4种走法，只能走一种，那么可以写一个迭代，假设进入1号走法，那么就进入新的dfs函数，此时再从1号走法的下一个位置开始继续dfs；

那么最终一定是有的方法有解有的方法无解，但无论怎样，最后一定会回溯到A点，此时就不用再考虑1号走法了，因为已经搜索（处理）了走1号以后所有的可能。

那么，将走1号时产生的变化全部还原到没有走1号的情况，然后继续迭代开始尝试2号。

同理，一次完整的迭代就将从A点开始走的所有可能都搜索了一遍，并且进行处理。

写在中间（？？？）

总之，上面算是大概讲了这2个算法，下面的内容都是根据实际问题了。会有模型的建立以及题目的分析。附带部分核心代码，但是整体上仍然是瞎bb了。

大概就是会列出一个模型，给出一个关于模型的通用解，有点类似高中物理的情况。当然博主也是菜的不行，肯定不能给出权威的分析，只是博主分析做过的题做出的简单总结归纳。

搜索路径的移动代码实现

一般来说，搜索问题是建立在图的基础上的。但是很多问题并没有使用图数据结构，而是利用数组在存放数据。

那么，我们对于在图上移动，就变成了通过移动下标从而在数组上移动。此时有2个问题：

简单的加n减n可能导致数组越界。
情况少可以写多个if枚举所有的走的情况，但是情况多会写非常多的重复代码。

举个栗子：A在迷宫中，可以走上下左右四个方向，那么如何模拟A走路的过程？其实这个是根据本身的代码来分析的。

一般来说，利用数组模拟图，那么数组的2个下标就是图的坐标，在图上移动就是坐标的变化。

那么我们可以将坐标的变化用数组来表示，例：

int map[5][5];

那么一个图map就建立完成了。总共有4种走法：上下左右。由于无法斜着走，所以对于i、j而言，上下左右移动时数值变化如下：

上：i-1,j
下：i+1,j
左：i,j-1
右：i,j+1

如何模拟上面的数值变化？此时需要的就是go数组了，4*2的二维数组，4表示4种可能，2表示坐标的总数。

迭代第一个下标，赋值第二个下标，就能完美还原n种走法。

struct person{
    int x,y;
};

int go[4][2] = { {1,0},{-1,0},{0,1},{0,-1}};

上面是标准的表示，用结构体储存位置，用go数组表示移动。

for(int i = 0;i < 4;i++){
    int new_x = per.x + go[i][0];
    int new_y = per.y + go[i][1];
}

go数组一般是二维数组，第一个4，表示有4个方向，第二个2表示是二维的地图。poj有个比较骚的题，三维迷宫，我们就要定义go[6][3]，因为有6个方向，三维的坐标。

关于是否是有效移动的写法

上一段是写了关于移动的相关代码，有一个非常重要的点没有写出来，那就是移动是否合法的问题。

最重要的一点是关于越界：假设有坐标(0,0)，在地图中，如果我们向上或者向左走，可以得到坐标(-1,0)和(0,-1)。可以看到直接越界了。那么我们必须来判断我们进行的一次移动是否是合法的移动。

为了整体代码的优美与简洁，单独将判定的算法写进一个函数是非常恰当的。我们无论怎样，移动后的数据是很少的，例如二维的地图，每次移动后的新坐标其实就是2个变量：x、y。

那么我们完全可以将x、y作为参数传递进入函数中再判断是否合法。合法返回值1，不合法返回0。

此时我们就先只考虑是否越界的情况，假设有地图map[5][5]，那么：

int check(int x,int y){
    if(x < 0 || x >= 5) return 0;
    if(y < 0 || y >= 5) return 0;
    return 1;
}

当然，我们也可以将或运算改成与运算，但是从逻辑上看，或运算显得更为简洁优美。

可以方便理解：每一个if语句都是一个限制条件，满足则不论，不满足直接返回0。那么有几个限制条件，我们就写几个if语句，如果所有的if语句都不运行，那么返回1，也就是说x、y是合法的。

所以，博主还是推荐大家这样来写check函数。（当然也有一些时间上的原因，博主之前写过几次与运算的函数，发现总会TLE，而改成或运算则没有这样的问题，具体原因确实不清楚，如果有懂的大佬欢迎评论告知）

另外，针对于题目的不同我们也有更多的要求，都可以写成if语句写入check函数，而判定的时候只用写一点代码即可，例：

// 通过路径移动获得新坐标(x,y)
if(check(x,y) == 0) continue;
// 下面的语句是对正确数据的处理

这也是为了代码的简洁。嵌套的层数越少，代码读起来就越容易，逻辑上也更清晰。

如果不满足，直接继续循环，不考虑下面的内容，而对正确的数据进行处理直接写在下面即可。

关于已经走过的点的存储问题

而现在，我们仅仅是判定了是否越界，搜索中还有一个非常重要的点，就是判定是否到了重复路径，或者说这个位置之前有没有走过。

这个是非常重要的，因为到了曾经走过的路（不是分叉点，分叉点在出现后就已经在考虑进入几个分叉的情况了，bfs已经将所有的分叉全部加入队列，dfs则是利用回溯回到选择之前）有可能出现死循环现象。

那么最终结果只能是内存泄露了。无论是否有剪枝，至少这一条路径不断地在进行操作而无法得到“解脱”。

这里可能有同学无法理解，分叉点到底标记不标记走过？这里解释一下：

如果是是bfs，在走到分叉点的时候已经将所有接下来要走的点全部放在队列里了。并且每次都是从队列中拿出新的点。也就是说分叉点已经无关紧要了，使命已经完成。所以加在“已经走过的点”是完全没问题的。

而dfs，因为有回溯，如果回溯的时候无法走到分叉点那就不能走另外的分支。

这点完全不用担心，bfs的算法框架在上面博主已经写过了，着重提示了在回溯的时候要取消上一步的操作。

假设我们用ver[][]数组来储存点的结构体，那么有这样的框架：

ver[now_x][now_y] = 1; // 记录分叉点已经走过
dfs(new_x,new_y); // 进入新的循环
ver[now_x][now_y] = 0; // 还原

确实，回溯的时候碰到了曾经的分叉点，但是我们在具体的一个分支中，这个分叉点一定要是走过的状态，只是在回溯后，我们需要将这个点还原，从而进入另外的分支。

所以，无论是bfs还是dfs，只要走过，直接加入“已经走过的点”集合就完全没问题，只是dfs考虑是否重置即可。

如何储存这个集合？其实非常简单，只用构造一个大小跟地图一样的数组即可，例如上面提到的ver[][]，博主更习惯写成step[][]，这个二维数组的两个维分别代表了x与y，那么走过的点令其赋值为1即可。

所以注意2点：

关于ver数组的初始化，一定要记得刚开始就初始化（否则每一位都是乱码），以及每一轮计算的开始初始化（上一次的运算结果清除）。

a> 使用memset函数即可：memset(ver,0,sizeof(ver));
在check函数中也要判定这个数组是否为1，如果是1，说明该点已经走过了，这样的数据也是不合法的。

关于记忆路径的几种写法

记忆路径，一般来说经常出现在题目的要求中，例如：走迷宫时找到一条最短路，同时输出这条路的走路顺序。

这样，等于说是额外将搜索时的路径给完整输出。

这个操作看起来并不是很难，但是代码的实现却是相当麻烦的。BFS与DFS有着不同的写法来实现记忆路径，分别来实现一下。

DFS 实现方案

DFS，因为利用了递归，所以看起来似乎对于记忆路径加一个回溯即可。真的是这样么？大家可以按照这个思路试一试。

直接写在代码里并不简单，因为回溯的时候不仅仅是找到正确路径后回溯，找到错误路径（例如迷宫撞墙）后仍然有回溯这个操作（所以在上面写DFS时进入递归后要在回溯的时候进行还原操作），如果简单地利用回溯最终输出的并不是正确路径，而是走过的路径。

但是我们仍然可以利用这个思路来完成记忆路径。

DFS有递归和回溯，那么我们可以利用队列。递归的时候将该路径添加进入队列。回溯的时候出队列。如果碰到目标路径（DFS达成满足条件时），就直接在if子句里处理即可。这个队列存放的就已经是目标路径了。

BFS 实现方案

BFS，相比DFS还是难一点的，一般用BFS的题也比较少同时要求输出路径。但是

曾经走过的路径，特殊的条件有特殊的写法

可以看一下poj的1321题：棋盘问题

这个题其实跟八皇后有点类似了，因为限制问题，横排跟竖排都只能放1个棋子。这就是一个特殊的限制条件——横排竖排只能有一个棋子。

先不想这个题，我们之前无论是DFS还是BFS都有一个重要操作——存储曾经遍历的点。

对于一个二维图而言，我们需要一个二维数组来存放这个走过的路径，但是对于这个题我们这样写就非常的麻烦。

空间上不是问题，问题是算法方面——假设第一行总共有3个位置可以放棋子，那么第一个棋子放下去后，该竖列跟横列就完全不能放棋子了。

我们只能将这个点加入二维数组，也就是说并没有利用这个特殊条件，明明知道这一横行跟竖行都不能放棋子，却还要在走一下。

同时又要写复杂的算法：

int check(int x,int y){
    int flag = 0;
    for(int i = 1;i <= MAX;i++){
        if(ver[x][i] == 1){
            flag = 1;
            break;
        }
    }
    if(flag == 1) return 0;
    flag = 0;
    for(int i = 1;i <= MAX;i++){
        if(ver[i][y] == 1){
            flag = 1;
            break;
        }
    }
    if(flag == 1) return 0;
    return 1;
}

回过头来，想一下八皇后我们是怎么写的：利用一个一维数组，ver[i]，表示第i列放了一个皇后，那么第i列就再也不能放皇后了。

跟该题是不是有点像？将二维数组化简为一维数组，ver[i]表示第i列已经不能再放了，至于具体是哪一行放的棋子我们不用管。

这样我们就能写出算法：

for (int i = 1; i <= n; i++) {
    if (maps[index][i] == '#' && ver[i] == 0) {
        ver[i] = 1;
        // dfs(index + 1, num - 1); 这句代码不是重点
        ver[i] = 0;
    }
}

for循环迭代的是该行具体已经在那一个位置放棋子，而ver[i]控制了哪一列不能放棋子。

所以说如果题目有特殊条件，就不能死板套模板，适当修改反而能写出优秀的代码。

DFS、BFS的形参列表的灵活运用

仍然是上面的题，这里

ACM搜索入门问题模型的构建与分析