链表有环及其延伸问题
首先,问题涉及的有环链表是指链表的尾节点不是null,而是指向链表中的其中一个节点,从而使得链表的其中一段是循环的,如果用图的话可以得到这样的数据结构:
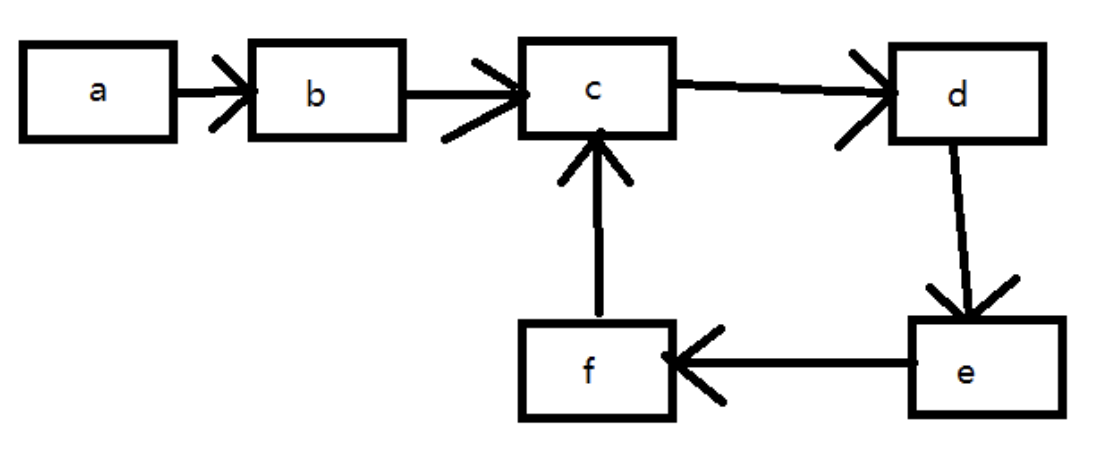
那么基于这样的数据结构有一系列问题需要处理:
- 判定是否有环,也就是说判定一个链表是否是有环链表
- 判定是否有环之后,又可以要求返回到底是链表的哪一个节点开始进入环的。
- 环的长度是多少,链表的总长度是多少。
- 反向思考,如果链表是无环的,那么给出两个链表的话,如何判定两个链表是否相交。
- 如果相交的话交点是哪个节点。
接下来就给出解决这些问题的算法。
然后,这篇博文用的语言是C++,然后测试用的链表就是上图,一样的结构。
而关于反向思考判定两个链表相交以及交点的问题,就不再写了,只给出代码。
链表节点的定义以及创建链表、测试正确性的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct Node {
int val;
struct Node *next;
}head,a,b,c,d,e,f;
void create_list() {
a.val = 1;
b.val = 2;
c.val = 3;
d.val = 4;
e.val = 5;
f.val = 6;
head.next = &a;
a.next = &b;
b.next = &c;
c.next = &d;
d.next = &e;
e.next = &f;
f.next = &c;
}
void test_link_list() {
Node *temp = head.next;
for (int i = 0; i < 10; i++) {
cout << temp->val << endl;
temp = temp->next;
}
}
这个。。。写的比较省事,不过也比较直白= =。结构体中val的值是指节点的编号,从1开始。
判定链表是否有环
如果是无环,那么在O(n)复杂度下遍历到null就说明无环。有环的情况下遍历是死循环的。
这个时候我们考虑利用遍历的速度差。例如高中物理经典问题“追及问题”,A、B两者的速度不同,那么在某个时间两者必定相遇。如果是在操场上赛跑,那么因为周期性,在n圈以后必定存在快的追及到慢的情况。
链表同理,如果同时从头开始用两个指针开始遍历,一个遍历速度慢(一次跳一个结点),一个遍历速度快(一次跳多个结点),那么只要保证:快速的能够整除慢速,也就是满足周期T的情况,那么一定能够在环上追及到。
那么,我们设定两个指针,最简单的方法慢指针每次跳1,快指针每次跳2,如果碰见null,说明链表无环,如果快指针指向结点与慢指针的一样,那么说明有环。这样在O(n)的时间复杂度内就可以得到解。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
int have_ring() {
Node *slow = &head;
Node *fast = &head;
if (fast->next != NULL) fast = fast->next->next;
slow = slow->next;
while (slow != NULL && fast != NULL) {
if (slow == fast) return 1;
slow = slow->next;
if (fast->next == NULL) return 0;
fast = fast->next->next;
}
return 0;
}
返回值是1说明有环,返回值是0说明无环。
快指针的速度问题
我个人认为快指针的速度是无关紧要的,对于一个固定的链表能在几次移动中判定是否有环,主要跟慢指针的速度有关,因为只有以最快的速度进环,才能保证相遇的可能。
而在环中,移动几次能够相遇又与慢指针的速度、环长有关。增加慢指针的速度,在一次就移动到相遇点的情况下,再快也至少要移动一次。
所以速度推荐慢指针移动1快指针移动2。
相遇点这个,因为在环上运动的话是周期性的,第一次两者相遇的话,那么下一次相遇必定还是在这个点。而如果交换两者移动的先后顺序到达的则是对面的点。
判定入环结点
既然判定有环,那么就能引申一系列环上操作,判定入环结点就是比较重要的。不过算法过程更偏向于数学推导验证。
还是上面的链表为例,图可参考最上面的。
我们假设链表的总长为L,链表头到入环点的距离为A,入环点到快慢指针追及点的长度为X,环长为M。如下图所示:
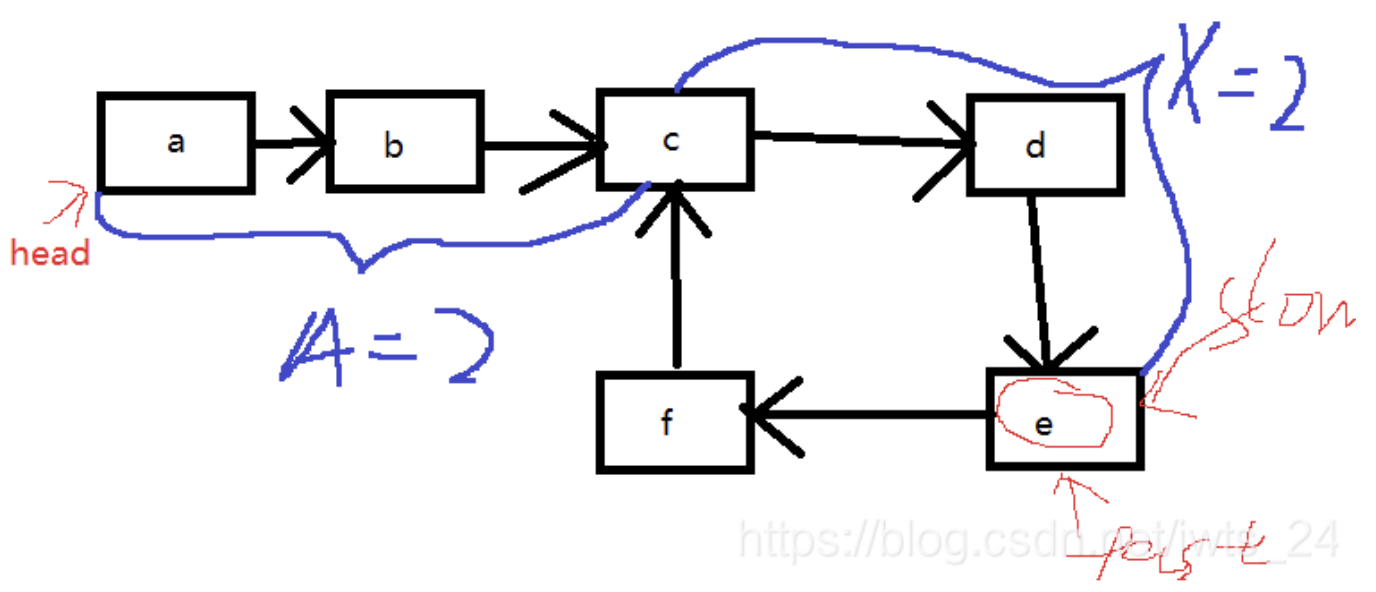
如果不论A这一段距离的话,从慢指针到达环上开始,到快慢指针相遇,因为慢指针绝对还没有绕环一周,也就是说X < M,如果快指针的速度是慢指针的两倍,那么慢指针移动长度2*X < M,也就是说快指针一定是没有超过两周。
而慢指针想要和快指针相遇,至少要绕环一周才可以。所以对于快指针而言,在环上的第二周碰到了慢指针。
这里分2种情况:
第一种:A < M。
此时,2*A < M,所以在慢指针进入环的时候,块指针一周还没有遍历完成,那么一定是在第二周与慢指针相遇,就像上图的情况,那么有:
\[\begin{align} L + X &= 2 \times (A + X) \\ L - A - X &= A \end{align}\]这里可以看到,L - A - X是相遇点到入环点的距离,和A是相同的。
第二种:A >= M。
此时快指针至少跑一周了,此时我们考虑一下截取,即按照周期M将多出来的部分给截取掉。例如这样的图:
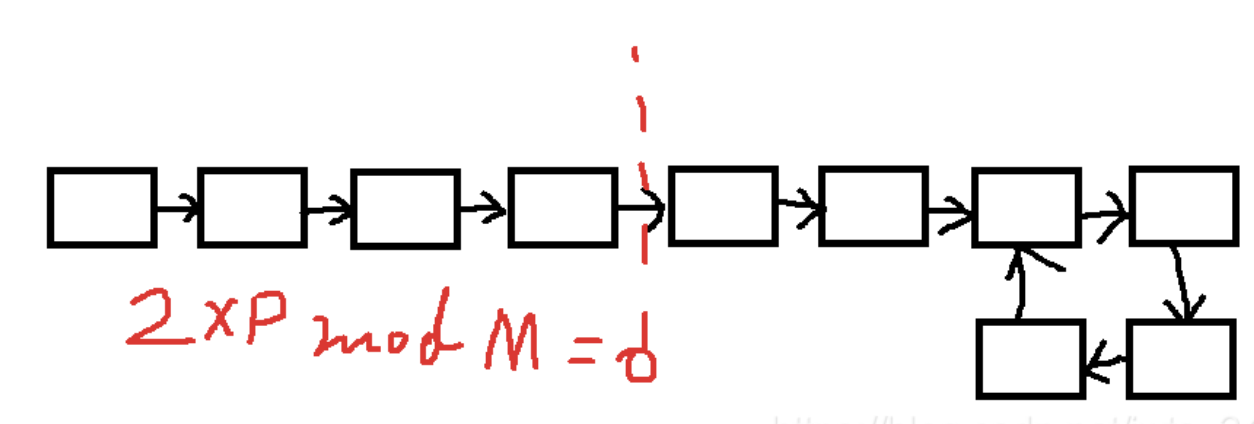
我们将其中多出来的P个结点,只要满足$2 \times P \bmod M = 0 $的情况,就可以想象成多出来的部分,慢指针还没有进环,而块指针在环上周期运动。
步数相抵消。那么就可以将P个结点截取,红线右边的部分就是上面的图了,就转换成了第一种情况。
同理,所有满足A >= M的链表都可以转换成A < M的情况。换而言之,都满足:L - A -X = A的情况。
既然满足这个条件,那么算法就非常简单了,设定两个指针,一个从head开始移动,另一个从相遇点开始移动,那么最终相遇的地方就是入节点了。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Node * get_ring_node() {
Node *p_head = &head;
Node *p_meet;
Node *slow = &head;
Node *fast = &head;
if (fast->next != NULL) fast = fast->next->next;
slow = slow->next;
while (slow != NULL && fast != NULL) {
if (slow == fast){
p_meet = slow;
break;
}
slow = slow->next;
fast = fast->next->next;
}
while (p_head != p_meet) {
p_head = p_head->next;
p_meet = p_meet->next;
}
return p_head;
}
有部分代码是重复的,这里是为了展示= =实际上最好是在判定是否有环的时候,就返回这个相遇点,如果相遇点是null说明无环,否则为有环。当做参数传递进函数就可以省略一部分代码了。
环长与链表总长
上面得到了这样的表达式: \(L - A - X = A\) 那么我们求的实际上是L与L - A。
首先在上面函数求入环结点的时候,遍历的数量其实就是A,这样我们就得到了A值。
然后如果我们继续遍历,从入环口开始,直到相遇点,统计这个遍历的次数就可以得到X值。
这样通过表达式的变式: \(L = 2 \times A + X\) 就可以得到L了。那么L - A也就可以直接获得。
这里注意链表总长的定义:一般我们指的是结点的数量,我们实际上计算的时候入环结点是计算了2次的,所以答案应该把多出来的给减去。代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int get_length() {
Node *p_head = &head;
Node *p_meet;
Node *slow = &head;
Node *fast = &head;
if (fast->next != NULL) fast = fast->next->next;
slow = slow->next;
while (slow != NULL && fast != NULL) {
if (slow == fast) {
p_meet = slow;
break;
}
slow = slow->next;
fast = fast->next->next;
}
int a = 0;
while (p_head != p_meet) {
p_head = p_head->next;
p_meet = p_meet->next;
a++;
}
int x = 0;
// 此时slow指针是指向相遇点没有变的
while (p_head != slow) {
p_head = p_head->next;
x++;
}
return 2*a + x - 1;
}
同上,还是将多余的写出来了。
环上长度就基本跟上面差不多了,将最后的$2 \times a+x-1$换成$a+x$就可以了。代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int get_ring_length() {
Node *p_head = &head;
Node *p_meet;
Node *slow = &head;
Node *fast = &head;
if (fast->next != NULL) fast = fast->next->next;
slow = slow->next;
while (slow != NULL && fast != NULL) {
if (slow == fast) {
p_meet = slow;
break;
}
slow = slow->next;
fast = fast->next->next;
}
int a = 0;
while (p_head != p_meet) {
p_head = p_head->next;
p_meet = p_meet->next;
a++;
}
int x = 0;
// 此时slow指针是指向相遇点没有变的
while (p_head != slow) {
p_head = p_head->next;
x++;
}
return a + x;
}
两个链表是否相交及交点
也是一个据说很经典的题,可以百度搜,原理以及解法可以看博主的另一篇博客:
这里就不多赘述了。
代码的重复问题
可以看到,上面很多代码是重复了很多的,因为这一系列的问题有很多重合点。但是如果我们能将入环点、相遇点给记录下来的话,就可以节省非常多的代码。
只用将这两个指针存进全局变量即可。这也比较简单,就是加两句代码的事也就不再写了(主要是比较懒= =)。