什么是最长公共子序列?
给一个poj的传送门:Common Subsequence
这就是标准的最长公共子序列了。
例如我们有2个字符串S1“abcae”与S2“acbea”,那么最长公共子序列就是“ace”。也就是说,子序列是按照顺序的,但是并不是连续的。
我们可以用动态规划的思想来完成这个算法。
状态分析
首先考虑我们应该如何分析“状态”以及状态的“值”。如果了解一点动态规划的情况下,对一个字符串(数组)的分析用一个状态数组就能表示。像斐波那契数列、最长上升子序列(LIS)。
那么求最长公共子序列的时候,我们给出了2个字符串,所以我们可以考虑用一个二维数组来表示。
以最长上升子序列为例,如果func[n]表示的是前n项中,最大的上升子序列长度的值,那么func[i][j]就可以理解为s1的前i项与s2的前j项存在最长公共子序列的大小。
这样的状态是有独立性的。我们可以看下图:
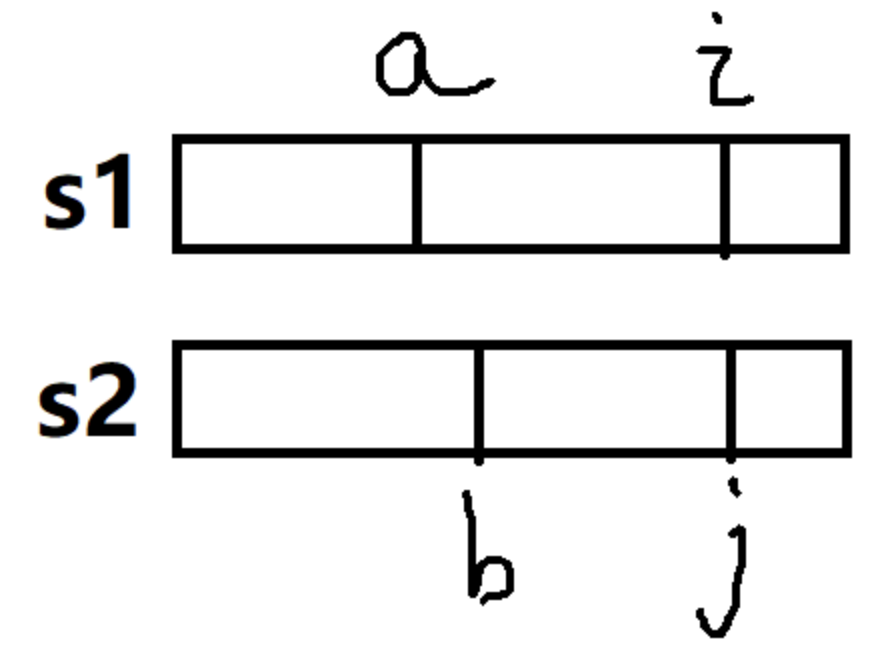
如果a与b恰好是终止点,即s[a] = s[b],同时拥有公共子序列。那么func[a][b]就是一个确定的值。
那么func[i][j]的值呢?如果a-i、b-j一个相同的字符都没有,那么func[i][j] = func[a][b],如果a-i、b-j其中一个存在公共的字符串,例如下面这种情况:
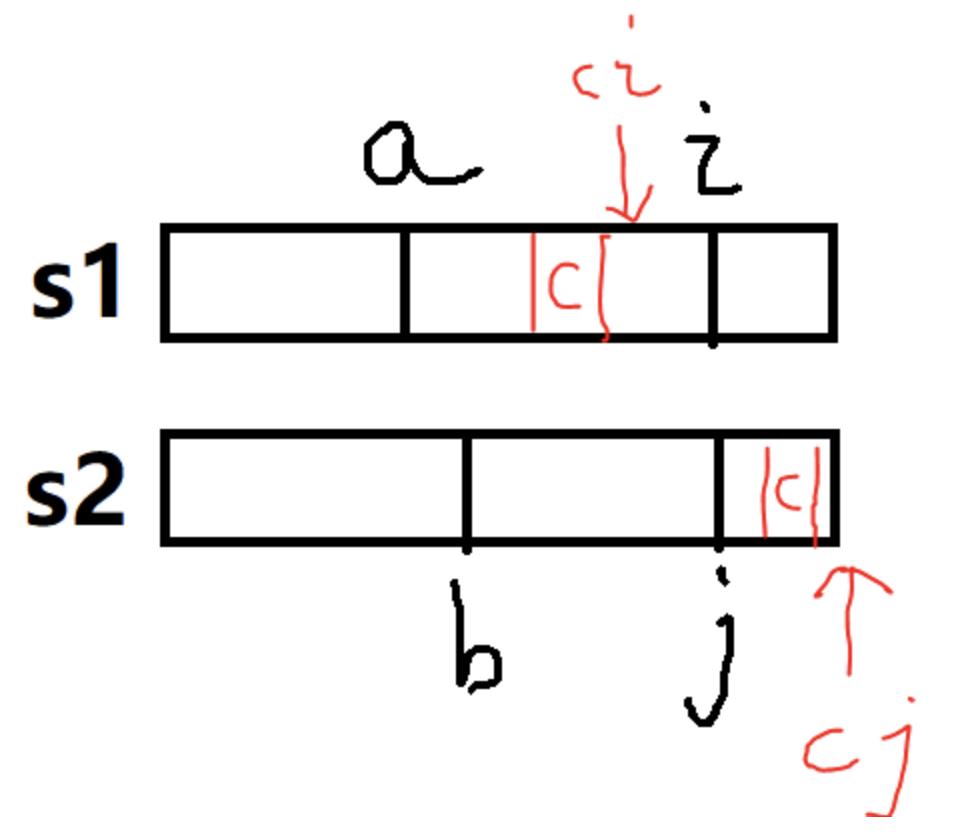
a-i中间有个字符c与j之外的恰好相同,那么func[ci][cj] = func[i][j] + 1。
所以说func[i][j]不收任何其他的状态的影响。虽然在i与j的范围内出现了与子序列不同的字符,但是这属于比该状态更上一级的状态。
同样,i、j的状态也跟a、b之后的状态无关,不管a、b范围内的字符串是怎样,都不影响i、j处状态的值。
由此,我们可以得出状态max_len[i][j],表示s1的前i项与s2的前j项的最长公共子序列的长度。
那么如果我们要求整个串的长度,那就是max_len[s1.size()][s2.size()]的值。
临界条件与递推公式
首先分析临界条件。极限很好找,max_len[i][0] = max_len[j][0] = 0。
在其中一个串是前0项的情况下,一定是0的。那么状态的取值范围就是0-i、0-j之间。我们可以得到二维数组如下:
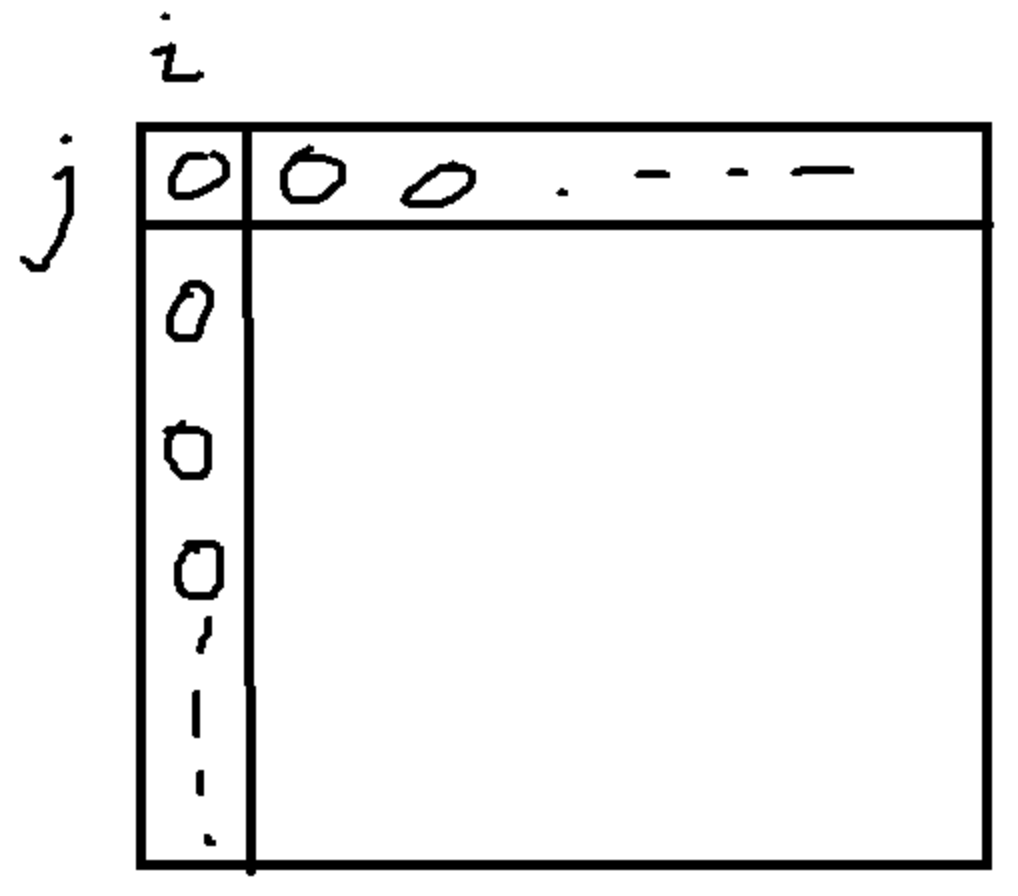
也就是说,我们的任务是填充这个二维数组,已知量就是上面填0的部分(想起来邓俊辉教授数据结构第一课就讲过这个,安利一下,b站就有全套视频,学堂在线搜索清华大学好像也有)。
此时我们再看状态数组。状态转移方程是如何写的?想一下斐波那契数列,fib[n] = fib[n-1] + fib[n-2],那么max_len[i][j]能否也向这样考虑?
可以看最上面的的图,如果令i-1、j-1,有2种可能,一种情况是不包括a-i范围内的c字符。那么max_len[i-1][j-1] = max_len[i][j],因为没有增加新的一样的字符对吧。
反过来考虑,如果s1[i-1] = s2[j-1],那是不是说明子串整体增加一位的时候恰好增加的相等,那么max_len[i][j] = max_len[i-1][j-1] + 1。这是相等情况的状态转移方程。
如果不满足上面的情况,也就是说s1[i-1] != s2[j-1],此时绝对是对max_len[i][j]没有影响的,看上图就可以知道,不管有没有字符c,i、j的状态不变。
那么在二维数组中,我们需要令max_len[i][j]等于一个值,这个值考虑max_len[i][j]的两个次状态(自创词。。),max_len[i][j-1]与max_len[i-1][j]。
那么这2个状态的最大值即是max_len[i][j]的值。所以有状态转移方程:
1
max_len[i][j] = max(max_len[i][j-1],max_len[i-1][j])
上面的如果不理解,多想一下二维数组的图理解一下。同样,关于二维数组的动态规划,我们都可以用这样的方式来得到状态转移方程。
这样,状态i、j就能够从i-1、j-1 i、j-1 i-1、j这3个状态中选择。那么我们从左上角(有3个0)开始遍历整个二维数组,最终就能填充完。
那么也很容易得到LCS算法的时间复杂度了:O(mn),其中mn分别为2字符串的长度。
模板题练一手,同时也是LCS模版
AC code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<iostream>
#include<string>
#define MAX 1000
using namespace std;
char s1[MAX];
char s2[MAX];
int max_len[MAX][MAX];
int Max(int a, int b) {
return a > b ? a : b;
}
int main() {
while (cin >> s1 >> s2) {
int len1 = strlen(s1);
int len2 = strlen(s2);
for (int i = 0; i <= len1; i++) {
max_len[i][0] = 0;
}
for (int i = 0; i <= len2; i++) {
max_len[0][i] = 0;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s1[i - 1] == s2[j - 1]) {
max_len[i][j] = max_len[i - 1][j - 1]+1;
}else {
max_len[i][j] = Max(max_len[i - 1][j], max_len[i][j - 1]);
}
}
}
cout << max_len[len1][len2] << endl;
}
system("pause");
return 0;
}