二叉查找树
关于性质之类的可以参考wiki、百度百科或者其他博客,其实也很简单,推荐看标准的描述。
而博主写的内容主要是想写成类似Map底层的。所以有泛型,并且是Key-Value结构。
关于二叉查找树,我们一般是类比二分搜索,仿佛跟Key-Value这样的结构并不一致。但是,在Java上,如果我们能在定义节点的时候,专门声明了Key与Value,并且在Key上定义comparator,那么就是通过对Key的排序,获取一个顺序序列,并且根据Key可以找到对应的Value。
这也是Java容器TreeMap与TreeSet的底层是红黑树的原因(其实差不多啦,红黑树可以自平衡)
那么如果说红黑树是二叉查找树的升级版,因为红黑树是保证平衡的,也就可以理解为什么Map的底层是一棵红黑树。我们这样来定义树,也可以完成Key-Value的模式。从而支持高效查找。例如下图:
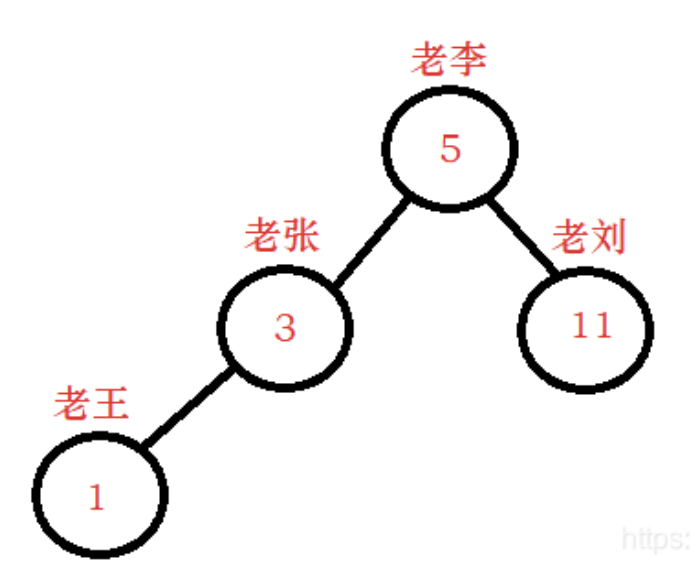
对于这些结点,编号就是Key,名字就是Value,如果设定Key的comparator,那么就按照编号来排序,在搜索某个编号的时候就能以O(logn)的复杂度搜索到对应的人的名字。
二叉查找树的定义与结点的定义
key与value是必须的,此外,要同时对key定义一个comparator。
由于Java语言,我们可以声明一个BST类,其中的内部类(或者可以专门写出来)可以有Node作为结点。那么可以这样来写:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class BST<Key extends Comparable<Key>, Value>{
private Node root;
private class Node{
private Key key;
private Value value;
private Node left;
private Node right;
private Node father;
public Node(Key key,Value value){
this.key = key;
this.value = value;
}
}
}
泛型是必要的,并且让Key继承Comparable,这样,我们在实际算法中,使用compareTo方法,就可以进行比较。
使用的话,先new出来BST对象,然后调用例如put、get方法等等,这个后面再实现。
关于father结点,如果是递归的算法,father就可以不用了,在回溯的时候就可以处理。但是非递归的算法,虽然也可以用last等来代替,但是并不好,推荐使用father结点,非常方便。当然也是一个额外开销(但是真的微不足道)。
二叉查找树的查找
很简单,就跟二分一样,从根开始搜,如果比该结点的key小,那么则进入左子树,大则进入右子树。
若相等,则表示搜索到了,若最终搜索到null仍未找到,那么就返回未搜索到。
自然,递归是非常简单明了的表现方式,但是递归的效率相对略低,但是比较容易理解。这里先写一个递归的写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public Value get(Key key){
if(key == null) return null;
return get(this.root,key);
}
public Value get(Node root,Key key){
if(root == null) return null;
int cmp = key.compareTo(root.key);
if(cmp == 0){
return root.value;
}else{
if(cmp < 0){
return get(root.left,key);
}else{
return get(root.right,key);
}
}
}
还是比较简单明了的,其实转化成非递归也非常容易:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public Value get(Key key){
if(key == null) return null;
return get(this.root,key);
}
public Value get(Node root,Key key){
while(root != null){
int cmp = key.compareTo(root.key);
if(cmp == 0) return root.value;
if(cmp < 0){
root = root.left;
}else{
root = root.right;
}
}
return null;
}
为什么要写get的两个重载方法?这样对于用户比较友好,用户只用输入Key就行了,其他一概不管。
主要是这样写,root就作为引用传入重载方法,那么我们对root的操作,不会影响到这棵树的真实root值。
这个是Java SE的内容,如果有疑惑的同学可以自己试试不用重载方法,会出bug的——在操作的时候,root对应的Node变了。
查找最大值与最小值
更简单了,一直向右子树前进直到叶子节点,就是最大值,反之则是最小值。简单的不行,就写个查最大值的算法:
1
2
3
4
5
6
7
8
9
10
11
12
public Value max(){
if(root == null) return null;
Node temp = max(root);
return temp.value;
}
public Node max(Node root){
if(root == null) return null;
while(root.right != null){
root = root.right;
}
return root;
}
查找的时候向下取整或者向上取整
这个略微麻烦一点,并且可能有点不太懂。
这个向上取整和向下取整是书上的翻译,感觉有点不合适,其实就是对于一个二叉查找树而言,查找其中的key为x的元素对应的value。
查找到了就返回,若没有查找到:返回比x小的最接近x的元素,或者返回比x大的最接近x的元素。
例如对于序列:[1,2,3,4,5,7,8,9]。如果搜索6,实际上是没有6的,那么向下取整方法floor(),的返回值是5,向上取整方法ceiling()则返回7。
整个算法有点蛋疼,但是我们以floor,向下取整方法为例,分析一下在搜索过程中可能碰见的几种情况,首先当然是从根开始,这些跟正常搜索一样,关键在于对根第一次匹配,如果小或者大了该怎么处理,抽象一下,对于任意子树的根节点,有几种判定情况:
- key = root.key。找到了,那就不多说,返回就完事了,没啥好说的,大团圆。
- key < root.key。此时小了,那么也就是说该树的根以及右子树完全不存在答案,我们应该从左子树开始继续搜索。但是需要明确一点,左子树中一定存在答案。那么直接搜left就行了,递归的话,就可以开始递归调用了。
- key > root.key。此时大了,那么也就是说,我们需要向右子树开始继续搜索。但是这里注意一点,root.key可能就是答案。
关于第三步,假设树的局部是这样的:
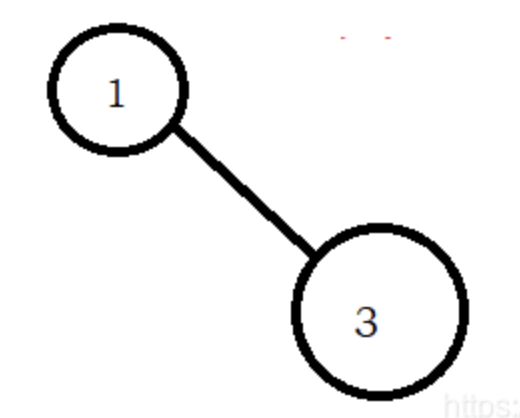
而我们搜索的是2。那么刚开始是1,进入右子树,而右子树是3,并且是叶子了。那么最终的答案是1。
但是如果3的左子树就是2呢,答案其实就是2了。所以说,在进入右子树的时候,root是有作为答案输出的可能的,所以需要记录root。
总结:找到就不说了,当进入左子树的时候,就是正常进入。当进入右子树的时候,需要临时记录root为res,如果res存在,则更新res。
这样分析,算法就比较简单了,而向上取整,就是相反,进入左子树的时候临时记录更新,右子树直接进入。
同样,没有写递归算法(当然递归是真的简单),仅仅实现向下取整floor:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public Value floor(Key key){
if(root == null || key == null) return null;
return floor(root,key);
}
public Value floor(Node root,Key key){
Value res = null;
while(root != null){
int cmp = key.compareTo(root.key);
if(cmp == 0) return root.value;
if(cmp < 0){
root = root.left;
}else{
res = root.value;
root = root.right;
}
}
return res;
}
插入
首先明白一点,根据二叉查找树的性质,插入的位置一定作为一个叶子结点,不可能是在中间进行插入的。
但是删除是可以从中间删除,甚至是删除根。但是这个是删除需要考虑的,一般删除的算法也是最麻烦的。
对于插入算法而言,首先是应该搜索——如果搜索到了,对于我们Key-Value这样的写法,是应该更新value的。如果没有搜索到,就new出来结点。
根据这样的情况,我们可以先搜索,再根据搜索结果判定如何插入。但是不能直接调用get(),而是应该手动实现。
自然,下面就不用递归写法了,直接写非递归的。当然,刚开始得考虑root为空的情况,此时直接new出来作为root。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public void put(Key key,Value value){
if(key == null || value == null) return;
if(root == null){
root = new Node(key,value);
return;
}
put(root,key,value);
}
public void put(Node root,Key key,Value value){
while(root != null){
int cmp = key.compareTo(root.key);
if(cmp == 0){
root.value = value;
return;
}
if(cmp < 0){
if(root.left == null){
root.left = new Node(key,value);
return;
}else{
root = root.left;
}
}else{
if(root.right == null){
root.right = new Node(key,value);
return;
}else{
root = root.right;
}
}
}
}
删除最小值与最大值
首先说明一下,删除相关的最好使用递归,写起来很简单。非递归方法也有很多,虽然思路一样,但是写法不同。博主的感觉有点不太好,仅做参考吧,感觉跟网上其他人写的相比好像多了很多判断的内容。
删除最核心的问题是:删除某个结点后,该结点的左右子树应该怎么办。
1962年Hibbard提出了现在一般使用的删除算法。这个算法首先需要先了解如何删除最小值与最大值。
首先比较容易想到的就是:一直左搜索就能找到最小值,一直向右就是最大值。
但是删除需要考虑的问题是,最大/小结点可能存在子树。
例如找最小值,一直左搜到最后的结点,该结点如果是叶子结点——直接删除,但是如果有右子树的话,就需要一些其他处理了。
另外,需要考虑如果删除的就是root,那么应该怎么操作——判定,按照特殊情况处理即可。
还是以删除最小值为例:在一路向左搜索直到碰见null,那么将右结点直接接到最小值的父结点即可,例:
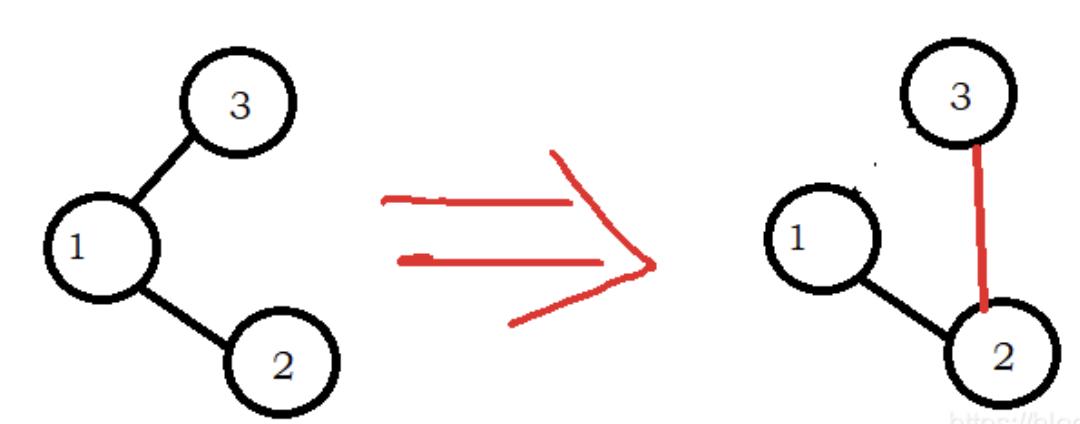
那么代码也就显而易见了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void deleteMin(){
deleteMin(root);
}
public void deleteMin(Node root){
Node res = min(root);
if(res.father == null){
this.root = null;
}else{
if(res.father.left.key.compareTo(res.key) == 0){
res.father.left = res.right;
}else{
res.father.right = res.right;
}
}
}
由于Java的垃圾回收机制,我们不用像C++那样释放内存,就这样不管就可以了。
说实在的,对于删除而言,不使用递归非常麻烦。父结点就算已经写进Node的属性中,但是无法确定到底是从左向下还是从右边连接下来。
而博主最早认为传递的是引用,直接对引用赋值等等,但是实际上是无效的,很疑惑。所以只能写if语句判断到底是应该调用left还是right。但是整体思路就跟上面的一样,实现就可以了。
如果是根节点,这个需要直接this.root = null。
关于父结点,博主是用last,不断更新父结点。这样是略微麻烦的,尤其是在删除的时候更麻烦。
如果没有对内存有过高要求,可以将父结点写入Node的属性中,会简化一部分代码。
删除
如果没有任何子结点,那么删除会相当简单(不考虑平衡)。删除难就难在如何确保两个子树能够被正确处理。
1962年Hibbard提出了现在用得比较多的一种删除算法。下面写的也是这种。算法分析了删除结点的3种情况:
- 是叶子结点。不存在两个子树,那么直接删除就行。
- 只有左子树或者右子树。直接删除结点,将子树续接上就可以。
- 同时存在左子树和右子树。这个也是最难的,下面详细谈。
不管怎样,只要有子树的情况,需要分析将子树怎么接上去,能够满足二叉树的条件。
对于只有单个子树的情况,可以看下面的图来理解:
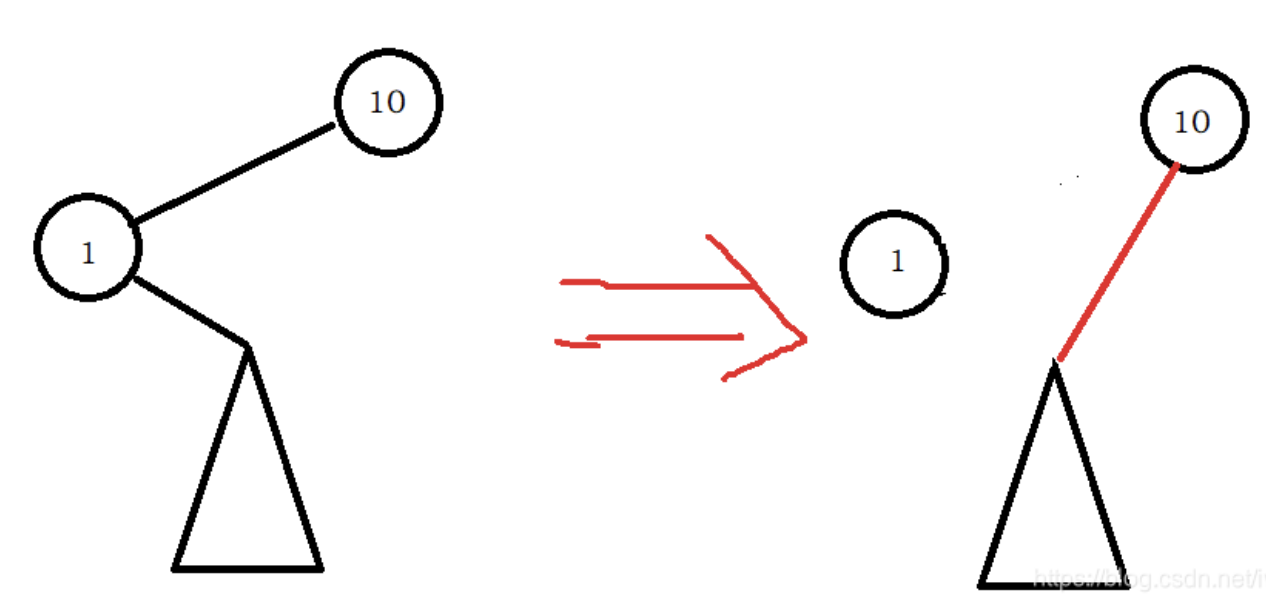
只存在右子树的情况下,右子树中所有元素必定小于删除结点的父结点。反之,左子树更是小于父结点。
如果删除结点实际上属于父结点的右子树,就是上面图的镜像,那么仍然满足,其子树完全大于父结点。
对于只有一个子树的情况下,删除结点的所有子孙全部满足二叉搜索树的性质,与父结点直接相连也完全满足。
但是如果有两个子树,就非常麻烦,因为我们直接相连的话,只能确保一个子树满足二叉搜索树的性质。
所以,下面详细说明第三种情况的算法。
剖析一下问题:删除之后面临的是两个子树无法满足二叉搜索树的性质。但是两个子树分别都是完美的二叉搜索树,换而言之,就是左右子树如何统一起来。
Hibbard给出的思路是这样:
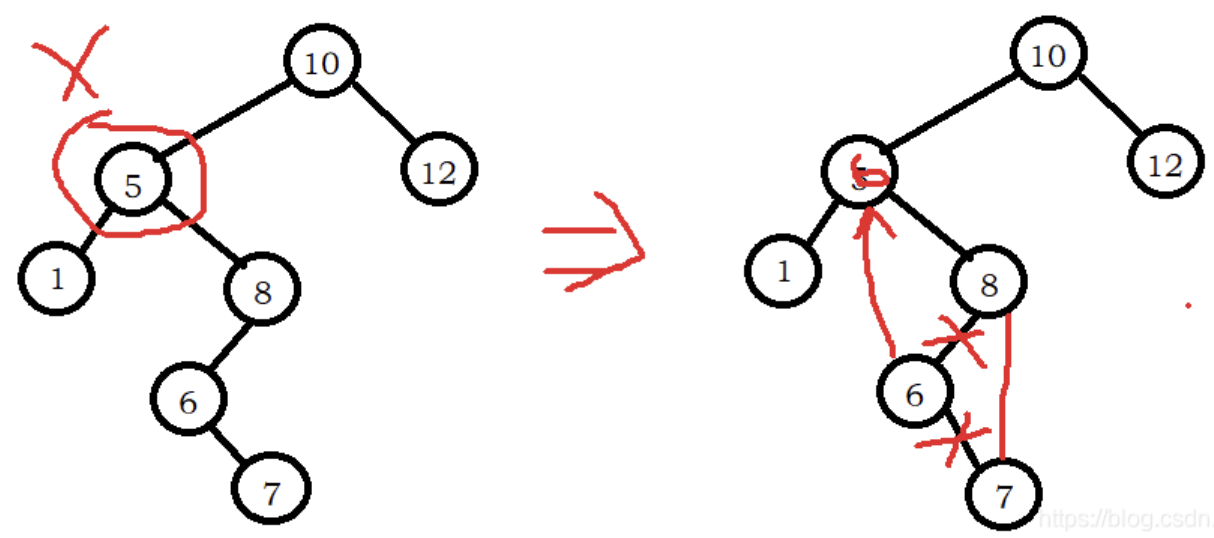
用文字描述:选择删除结点的右子树中最小结点来代替删除结点。
而假如这个最小结点还有右子树呢?就像图中的解决方法,其实就是上面的deleteMin,删除最小结点的算法。
原理是这样,删除结点需要被代替,而这个代替的结点的值必须满足这样的条件:大于左子树中所有结点(除了本身),大于右子树中所有结点(除了本身)。
那么选择就很简单了,只有2个结点满足:左子树中最大结点或者右子树中最小结点。
当然,博主选择了后者,如果非要用左子树中最大结点代替,完全ok。
那么对后续的处理恰好跟删除最大/小结点的算法一致,那么我们只用将需要删除的节点的值用这个代替节点来代替就可以了。
那么在实现上:我们可以搜索右子树的最小值,然后按照上面的处理方法处理好结点之间的调用关系即可。这个说起来似乎不难,但是代码非常多。
有一点,就是关于代替。我们可以这样:不修改任何连接,删除右子树最小结点后已经返回该结点了,然后将key、value等直接修改被删除结点。而另外的算法就是修改引用,完全被代替。
这个应该视具体情况而选择,取决于Node中属性的数量与修改后是否影响很多。当然,代替很简单,博主写的是修改引用的算法。所以仍然需要保存父结点。
代码感觉有点多了,因为Node是内部类,而root写进BST的原因,需要单独处理删除根节点的情况,所以代码可能比较多。
但是思路跟上面一样,调用之前写过的min跟deleteMin两个方法。中间很复杂的,其实不难,就是各种将引用调对。将上面的树代入走一边就可以理解了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
public void delete(Key key){
if(key == null) return;
// 删除根的情况,需要额外处理
if(key.compareTo(root.key) == 0){
if(root.left == null && root.right == null){
root = null;
}else{
if(root.left != null && root.right != null){
Node temp = min(root.right);
deleteMin(root.right);
temp.left = root.left;
temp.right = root.right;
root = temp;
}else{
if(root.left == null){
root = root.right;
}else{
root = root.left;
}
}
}
}else{
// 其他情况
delete(root,key);
}
}
public void delete(Node root,Key key){
// flag处理方向,父结点是从左子树连接下来还是右子树
int flag = 0;
while(root != null){
int cmp = key.compareTo(root.key);
if(cmp == 0){
Node father = root.father;
if(root.left == null && root.right == null){
if(flag == 1){
father.left = null;
}else{
father.right = null;
}
}else{
// 核心算法部分
if(root.left != null && root.right != null){
// 找右子树最小结点
Node temp = min(root.right);
deleteMin(root.right);
temp.left = root.left;
temp.right = root.right;
temp.father = root.father;
if(flag == 1){
father.left = temp;
}else{
father.right = temp;
}
}else{
if(root.left == null){
if(flag == 1){
father.left = root.right;
}else{
father.right = root.right;
}
root.right.father = father;
}else{
if(flag == 1){
father.left = root.left;
}else{
father.right = root.left;
}
root.left.father = father;
}
}
}
return;
}else{
if(cmp < 0){
root = root.left;
flag = 1;
}else{
root = root.right;
flag = 2;
}
}
}
}
按顺序打印
其实是树的遍历,因为二叉查找树的性质,中序遍历获得的就是递增的顺序。
树的遍历并不是二叉查找树独有的,代码就不写了。递归吧,简单粗暴,当然也可以用队列。说白了就是看BFS跟DFS用哪种搜索罢了。
按范围查找
刚看见这个的时候突然想起来以前比赛倒是有个题是这样= =当时记得是用树状数组做了吧,二叉查找树也可以。
思路很简单,在进行中序遍历的时候进行判定,不断进行剪枝,缩小范围,直到搜索到最底层。整体时间复杂度O(nlogn)可以接受。
将遍历的结果扔队列吧,也可以。这个就不写了。
关于自平衡
好像叫查找树的线性化?大概就是这样,如果我们按照标准降序或者升序进行插入,那么最终得到的树,只有一个叶子,横过来就是一个线性表。
也就是说,对于二叉查找树,各种操作的时间复杂度并不是严格的O(logn),而是最优情况下为O(logn),最坏情况下为O(n)。
而O(logn)的比较直白的解释是:如果是满树,那么树高度为$\sqrt{n}$ 。这就引出了树的平衡性概念。
如果我们在基本的操作中,能够添加一些内容,保证二叉树可以完成自平衡,就能杜绝线性化,保证不管数据如何操蛋,最终都是跟二叉树一样,能够在O(logn)的复杂度下运行。
AVL树是其中一个可以自平衡的树,当然红黑树是完美的黑树平衡。
那么二叉查找树了解之后(因为不管是AVL树还是红黑树,大量操作都跟二叉查找树有关),可以看一下2-3树,了解一下理论,2-3树或者是2-3-4树其实是有点理论化的,或者说是抽闲的数据结构,有很多其中的实现,例如B树、AVL树、红黑树等等,用了大量的2-3树、2-3-4树的理论。
完整的Java代码
可以看我的Github,提供了一个简单的数据结构模版,在main方法中,直接用put给加上去了。
| [BST 模版 | iwts’s Github](https://github.com/iwts/data-structure/blob/master/binary-search-tree.java) |